What Is Expected Value?
Expected value (also known as EV) is the average outcome of a bet or event after factoring all possible outcomes and their probabilities.
Expected value essentially tells you whether a bet or other investment is a good and profitable decision. It is often used in both the gambling industry and in finance to help determine if an investment or bet is worthwhile by assessing potential risks and returns.
It might sound complicated at first, but you can use expected value to help you profit from Matched Betting to ensure you make the right decision for each bet you place.
In this article, you’ll learn why we use expected value in betting, how to easily find positive expected value bets and discover the best strategies that can help you make huge profits this year.
What Is Expected Value In Betting?
In betting, the expected value (EV) is a measure of the potential value or profit that a bet can make over the long run, taking into account both the probability of winning the bet and the potential payout.
Put simply - it helps you know if a particular bet is worth it or not.
This doesn’t mean every good value bet will win and likewise, it doesn’t mean that every poor value bet will lose.
Profitable sports bettors know and understand this - A positive expected value (+EV) bet means that you would expect to make money on the bet in the long term. While a negative expected value bet (-EV) means you would expect to lose money in the long term.
Expected value is how bookmakers and casinos make money - the majority of bets they offer are -EV to punters meaning the bookies and casinos are taking the opposite +EV bets. They don't mind if they lose in the short term because they know with mathematical certainty that they’ll profit in the long run by taking a large number of +EV bets.
How To Calculate Expected Value In Betting
When Matched Betting you’ll never need to calculate the expected value yourself as this is all done for you with Outplayed. However, it’s helpful to see where the value comes from.
To calculate the expected value, you multiply each possible outcome of an event by its probability of occurring, then add up all those results. This will give you the average outcome you can expect if you were to repeat the event many times.
Let's say you're playing a game where a fair coin is tossed and if it lands on heads, you win £10 and if it lands on tails you lose £5.
There’s an even chance of winning and losing - you have a 50% chance of it landing on heads and winning and a 50% chance of landing on tails and losing.
You can calculate the expected value of this game by doing the following:
EV = (0.5 x £10) + (0.5 x -£5) = £5 - £2.50 = £2.50
The EV for this game is £2.50. As this is a positive number, you have a +EV opportunity.
This doesn’t mean you’d win £2.50 every time you played in the short term but if you played this game an infinite amount of times you would expect to make an average of £2.50 each time you play it.
The Importance Of Variance
Variance reflects the random nature of a game in short bursts and is an important factor when considering expected value.
Let's consider flipping a coin - If we flip a coin once, we have no idea if the result will be heads or tails and if we flip it 10 times in a row, we might guess that around 5 would be heads and 5 would be tails - but the reality is we might get heads 6 or 7 times out of the 10. We wouldn't find that particularly surprising. And if we did it again we might get tails more often than heads. This is called variance.
But if we flip the coin 1000 times in a row, we would likely get heads around 50% of the time, give or take. This means that variance becomes less of a factor the more flips you complete, and the Return to player (RTP) becomes the thing that matters.
Return to player (RTP) is the percentage of wagered money that a game is expected to pay back to you over time.
How Is Expected Value Used For Matched Betting?
Expected value is important in Matched Betting as it allows you to identify profitable opportunities. By calculating the estimated value you’ll know which bets and offers are going to make you money and are worth doing and which ones to avoid.
You’ll not be able to lock in a profit like with the sportsbook signup offers but as you can see from the example above, it’s in your interest to take +EV opportunities to profit over the long run.
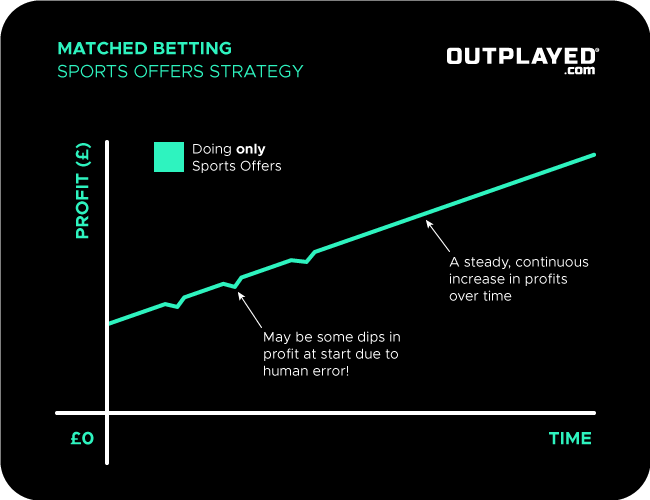
Rather than a steady, continuous profit over time, your profit over time graph for expected value offers will be similar to the casino offers strategy by only doing +EV bets and offers.
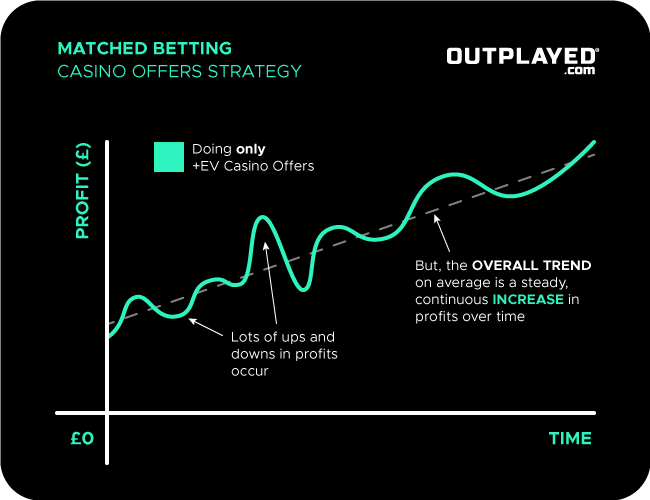
Positive expected value Matched Betting opportunities come in a variety of offers ranging from low risk to high risk and you can choose which you focus on depending on your experience and the size of your Matched Betting bankroll.
Take this low-risk daily offer from The Pools for example. By placing £25 worth of bets on virtual sports (these are simulated events) you’ll get a free bet to use.

You cannot lay off virtual sports bets so your initial £25 is at risk but you can break the £25 into smaller stakes to reduce the variance of the offer.
By knowing the return to player (RTP) of the virtual sports games, we can work out the expected value of this offer and in this case, it’s £1.95.
So by doing this offer in the long run, you can expect to make around £1.95 each time. There are tons of +EV offers available and committing to a large number of them whilst managing your bankroll will yield amazing results.
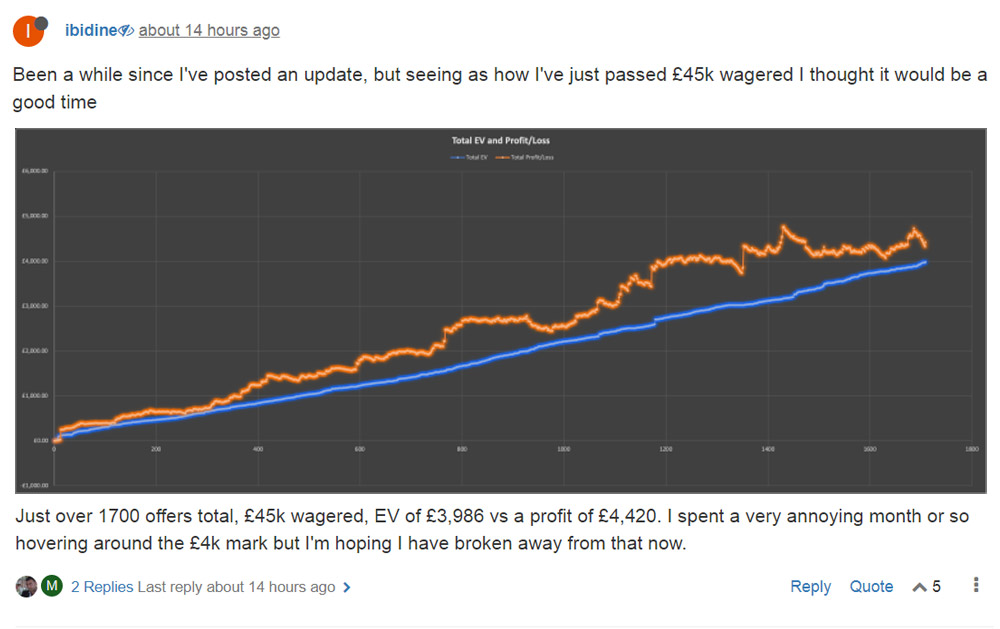
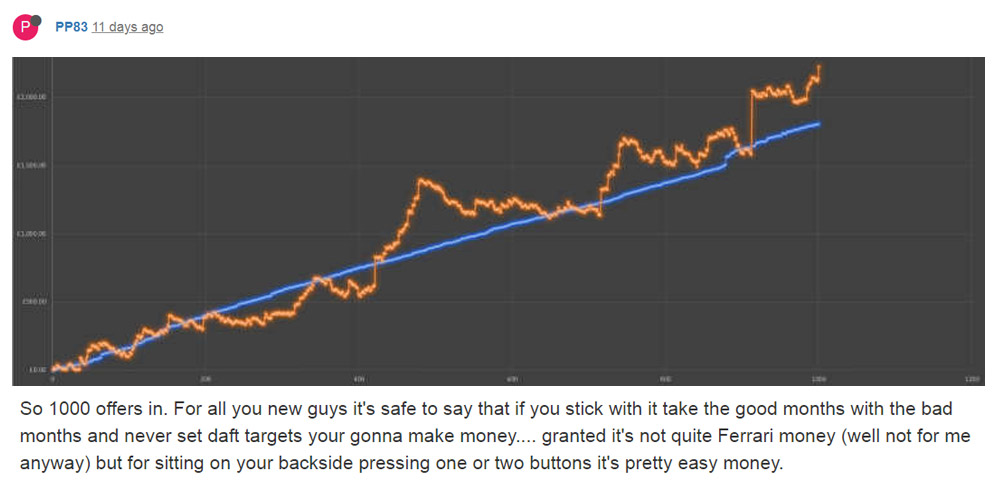
Check out these two Matched Bettor’s results, the blue line represents the total amount of EV taken vs the red line shows the actual amount of profit made:
How To Find Expected Value Bets?
The easiest way to find expected value bets is to use a Matched Betting service such as Outplayed.
You can find profitable value bets throughout the Outplayed site such as the reload offers section - here you’ll be presented with all the best +EV offers available each day without having to check terms and calculate the expected value of each offer yourself - you just open the guide and follow the step by step instructions.

To boost your profits to the next level you can also quickly and easily find expected value bets using more advanced tools available with Outplayed Pro which allows you to take a huge amount of value each day.
These advanced tools use special algorithms to identify which bets have a positive expected value leaving you to simply place the bets and bank the value.
What Are The Best Expected Value Offers And Betting Strategies?
There are a range of different offers and strategies to extract expected value from bets. Ideally, you’ll include a range of these strategies to ensure you’re taking maximum value but you can start by using lower-risk strategies first until your bankroll and experience has grown.
Casino Offers Strategy
A great way to begin taking advantage of expected value is to use low-risk casino offers - these can be casino signup offers or reload offers listed on Outplayed available with the Diamond membership.
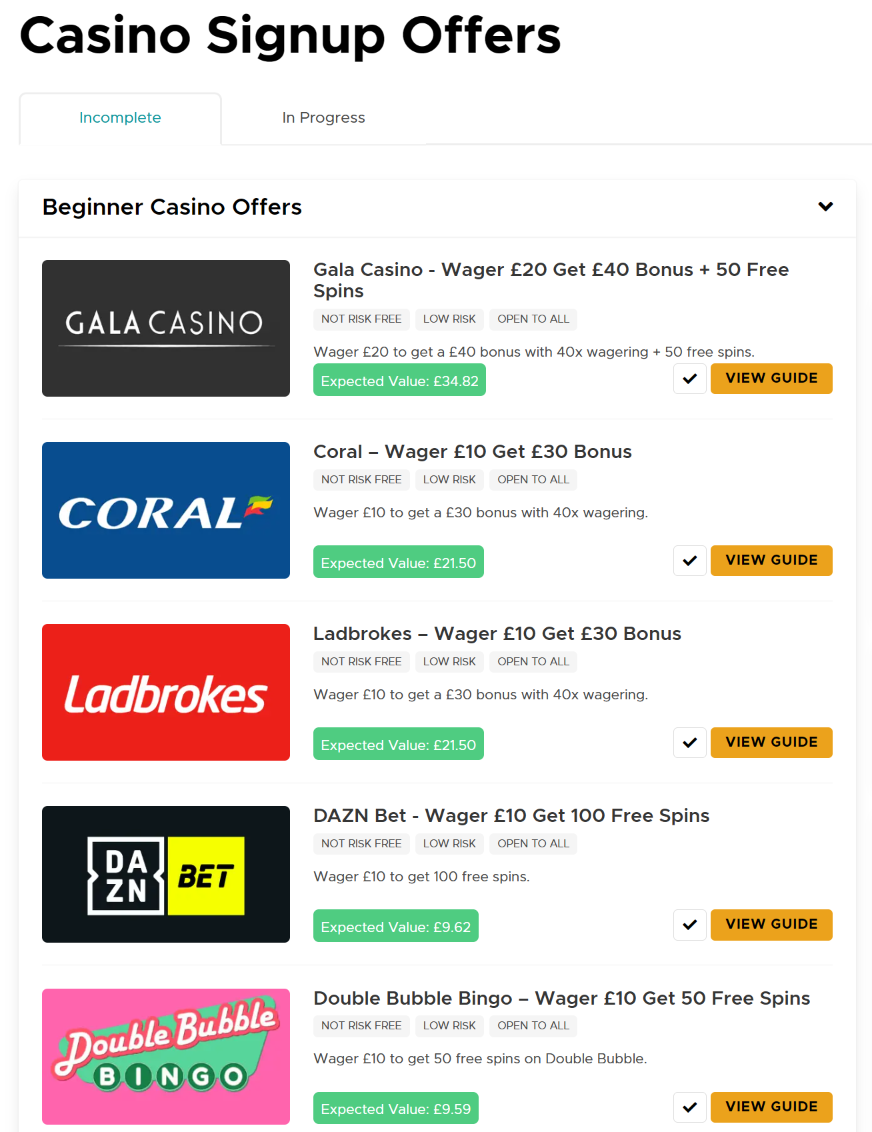
Unlike with Matched Betting sports offers, you’ll not be laying off bets when doing casino offers. You can’t lay off a spin on a slot machine. There is no ”casino betting exchange” when doing casino offers.
The key foundation of the casino offers strategy is that you’ll only ever do offers that have a positive expected value.
You don’t need to worry about finding these offers or how to do them as each +EV casino offer listed has been checked and tested and comes with full instructions on how to complete them.
As you build your experience and bankroll you’ll be able to move to medium and higher-risk casino offers to take even more EV.
Horse Racing Extra Places Strategy
Extra Place offers are a popular horse racing offer available at many bookmakers.
An “Extra Place” is when the bookmaker says they’ll add one (or more) additional places to their standard place classification on a particular race.
So, for example, they may offer to “pay 4 places on a race” instead of the standard 3 places. The 4th position in this instance is then the “Extra Place”.
You can place a matched bet so if your horse finishes in that 4th position in a race (the “extra place”) – you make money – and usually pretty good money too!
Experienced Matched Bettors are using the powerful Extra Place Master tool available with our Outplayed Pro membership to make an easy £500+ a month from these Extra Place offers.
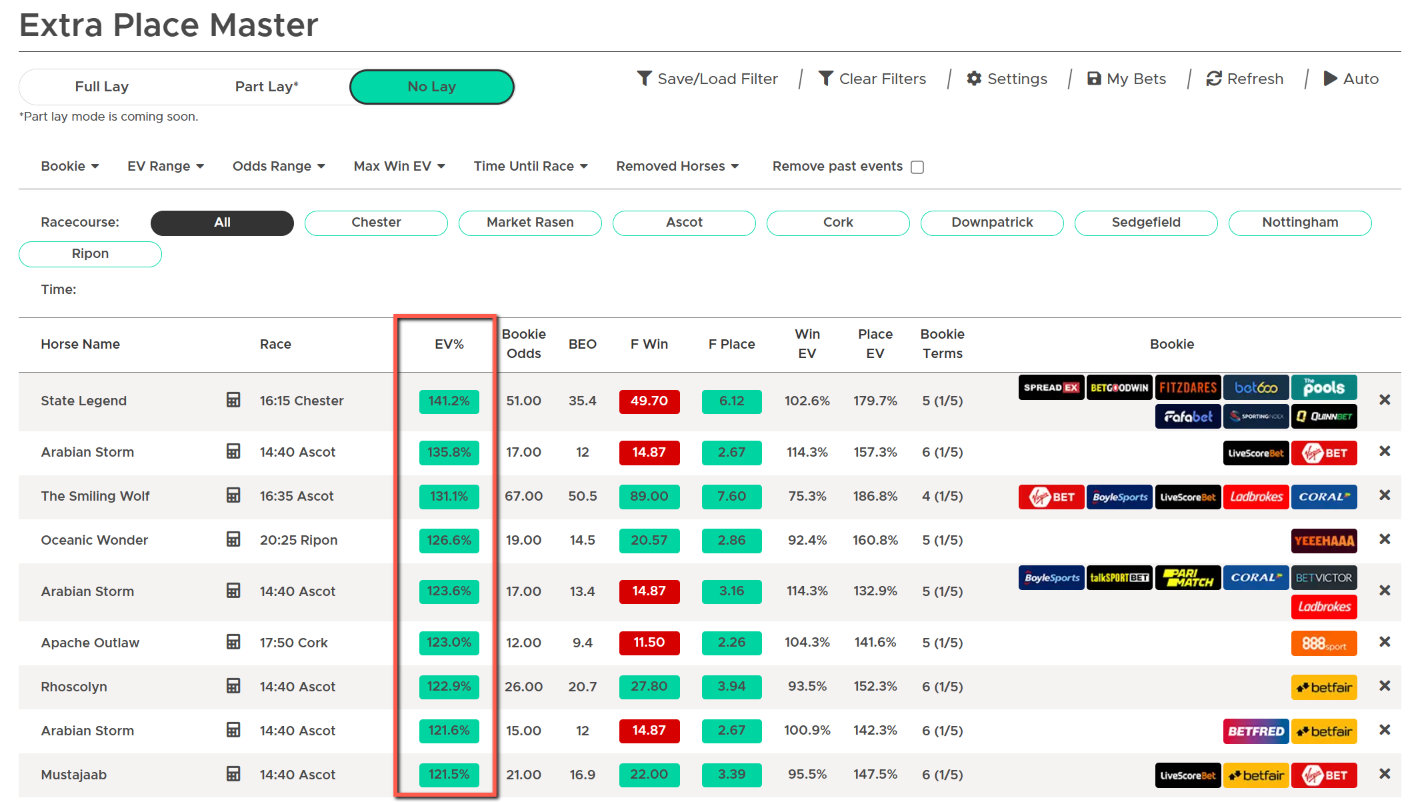
The beauty of this strategy is that you can use a method which suits your tolerance to risk. You can choose a lower-risk method of laying your bets to take a small qualifying loss and make a profit if your horse finishes in the extra place position.
Alternatively, you can use a higher-risk method with higher long-term returns using the no lay method to simply place back bets on +EV horse bets to profit in the long run.
The no lay method is very high risk so only suitable if you’re experienced and have a large bankroll that can take the swings in profit.
2up Early Payout Strategy
2up Early Payout offers are a football promotion where a bookmaker offers to pay your bet out as a winner (in cash) if your team leads by 2 goals at any point in the match (unless a different payout trigger is stated).
Using Matched Betting can mean huge potential profits if your team leads by 2 goals but then fails to win the match. The key is finding the right expected value bets that are profitable long term and our revolutionary 2up Master software makes finding these 2up early payout opportunities a breeze.
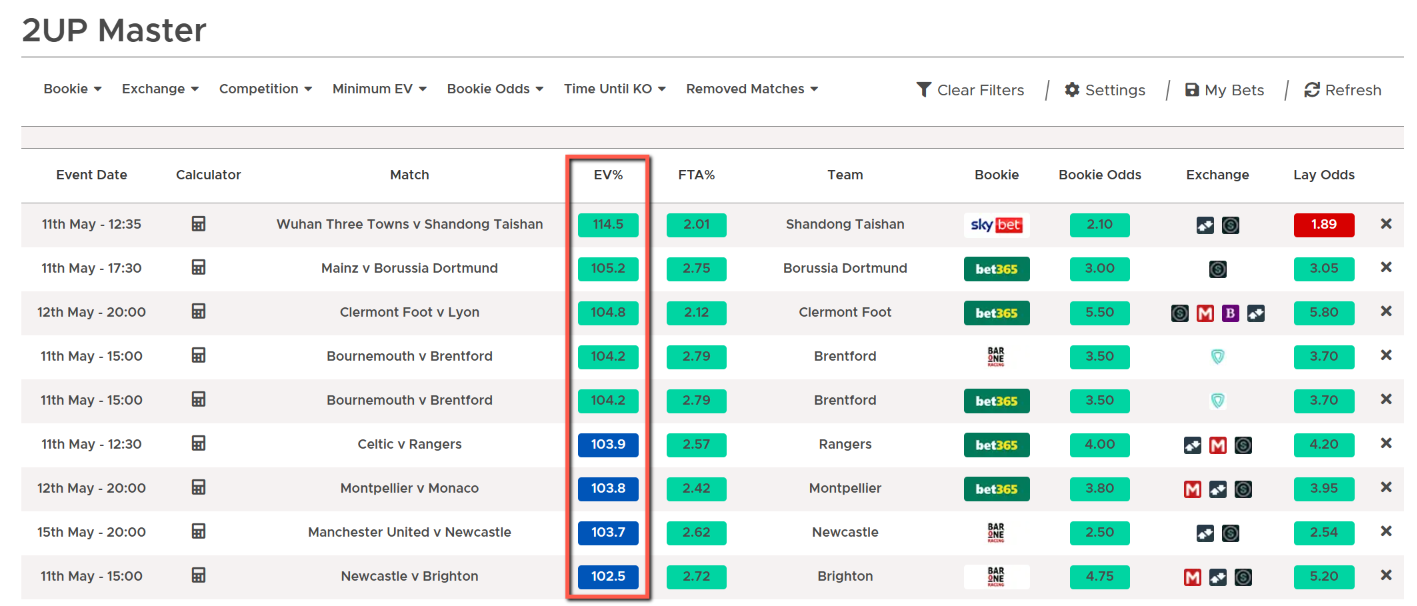
The 2up Master available with Outplayed Pro uses an algorithm that factors in thousands of data points including scoreline data, momentum effects, home/away advantages and more. This means you’ll know which bets have a positive expected value (EV) and are worth doing and which ones aren’t.
Lucky Finder Strategy
The number one strategy in terms of taking the most EV is the Lucky Finder strategy. This strategy involves placing accumulator-style bets called lucky 15 bets to compound value which results in the overall expected value being much higher.
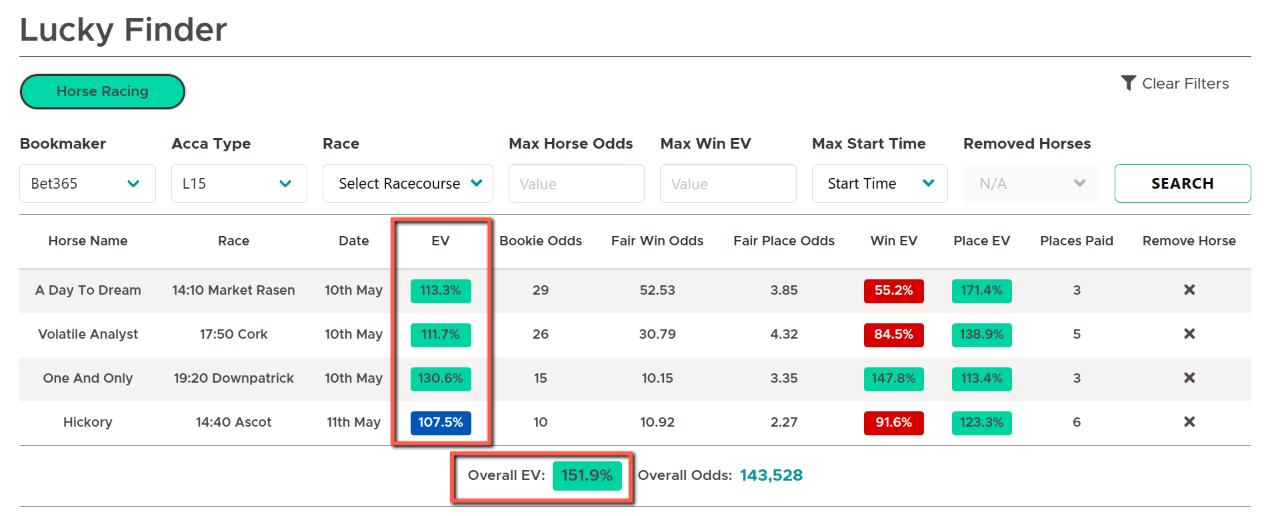
In addition to unlocking a ton of value, placing these value bets can also help you avoid being gubbed by looking more like a regular punter. You’ll also be able to use your gubbed and restricted accounts to place these bets meaning you can take value from bookmaker accounts you thought were no use.
The Lucky Finder - available with Outplayed Pro - accurately finds profitable lucky 15 bets for you in an instant and you don’t need to do any calculations yourself, you simply choose a bookmaker and the software will show you four selections to add to your bet slip and place your Lucky 15 bet to take the stated expected value.
You can then repeat the process using the same or other bookmakers to place multiple bets throughout each day to take a crazy amount of EV.
Summary
You’ll now see how important expected value is when making any financial decision and how you can apply that to your betting to ensure you profit over the long run.
The great news is that you can use offers to lock in profits to accompany your value betting to help smooth your variance and boost how much you can make from Matched Betting.
Interested In Getting Started Matched Betting?
You can start learning for free with our free trial and make your first profits today!

Updated: 18 Jul 2024
The Author
Ben is an expert in Matched Betting with nearly a decade of hands-on experience. He enjoys sharing his knowledge and is dedicated to creating high-quality, beginner-friendly content that educates and informs readers about the amazing opportunity that Matched Betting is.
Recent Posts
Kelly Criterion Betting System: Optimising Bet Stake SizesHow Long Does Matched Betting Take?Is Copywriting A Good Side Hustle? A Complete Guide For 2024What is Mug Betting?Is Matched Betting Tax Free? Everything You Need To Know
