Martingale Strategy: Does It Work? Insights
The Martingale Strategy is one of the most famous betting systems ever created, promising an almost irresistible allure: if you just keep doubling your stake, you’re bound to come out ahead eventually, right?
Imagine sitting at the roulette table, on the brink of victory or disaster, each spin seemingly bringing you closer to triumph—or deeper into the red.
The idea sounds simple, and in theory, it even seems foolproof. But why, then, do casinos not only allow it but welcome it?
You can certainly give yourself a long-term edge at online casinos by taking advantage of their numerous casino offers. In this article, though, we’ll dive deep into the Martingale Strategy’s history, its appeal, and, most importantly, the harsh reality behind why it’s not the golden ticket it may appear to be.
Before you place your next bet, read on to learn why this system could lead to more losses than you might expect.
What Is the Martingale Strategy?
The Martingale Strategy is a betting strategy where you double your wager if you lose, and return to your original stake if you win.
It’s usually used for bets that pay twice your stake if you win, for example betting on red or black in roulette, or sports bets at evens (2.0 odds). We’ll concentrate on red/black roulette bets here.
Let’s imagine you’re playing roulette at the casino, with a £10 chip on black for your first wager.
The croupier declares ‘no more bets’ and spins the wheel. After jumping around chaotically, the ball looks to have settled in the black 26 pocket, but bounces out at the last minute and ends up in red 19, leaving you £10 down.

Normally you’d just about to put another £10 chip on black, but you remember an intriguing system you’ve read about that seems to give you a surefire way of ending the night in profit. Even if you win wager another £10 and win, you’ll only cover your existing loss and break even over the two wagers. But what if you double your stake to £20?
Then, if you win the next wager, you’ll be £20 up for the round, covering the loss from the previous round and giving you £10 profit on top.
With this in mind, you double up, sliding two £10 chips onto black this time. Again, the wheel spins. Again, it lands on red. Another £20 loss, and you’re now £30 down overall.

No problem though - if you double your stake to £40, a winning bet will give you £40 profit. This will cover your losses of £30 and leave you £10 up overall.

This time, you’re in luck - the ball comes to rest in the black 29 pocket, and you win £40.
Not wanting to push your luck any more, you cash in your chips and leave the casino £10 richer, pleased with yourself for turning a losing position into a profit.
The system you’ve used is called the Martingale Strategy, or Martingale System, and it’s been around for well over 200 years. It’s easy to describe in a few words:
If you lose, double your stake. If you win, bet your original stake.
The idea is that, as long as you eventually have a winning bet, you’ll always cover your previous losses plus a profit equal to your original stake.
Below are a few possible winning runs using the Martingale Strategy, betting on black at the roulette table and starting with a £10 stake.
Example 1 - 1st Bet Wins

Example 2 - First two bets lose and 3rd Bet Wins

Example 3 - First three bets lose and 4th Bet Wins
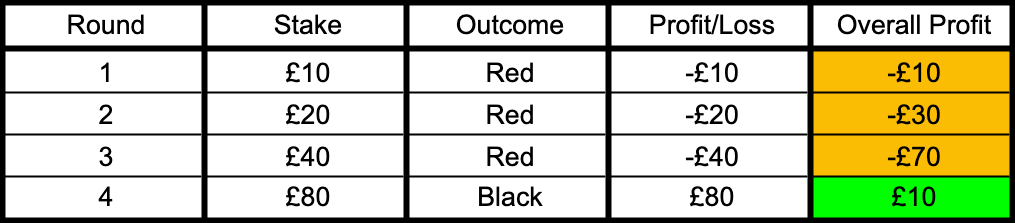
In each case, you’ve come away with a £10 overall profit by doubling down until you get a winner. After each winning run, you’d return to your original £10 stake for the next wager.
The table below shows that no matter which spin you win with, your overall profit will be equal to your original stake. That’s assuming you have a winning spin, of course. This example uses a more modest £1 starting stake:
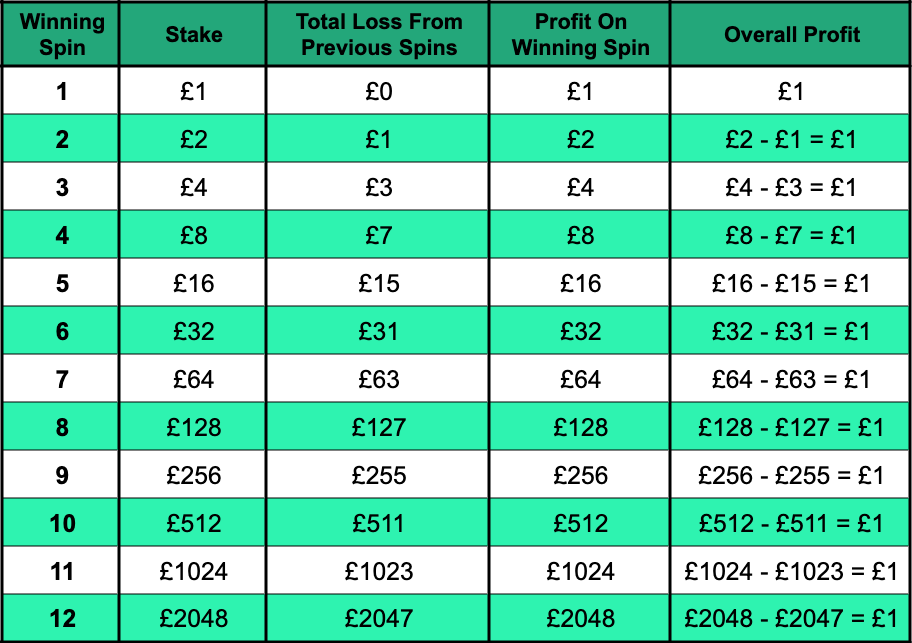
For example, if you lost the first 7 spins, your total loss so far would be the sum of the previous losses:
Loss on First 7 Spins = £1 + £2 + £4 + £8 + £16 + £32 + £64 = £127
Your stake on the 8th spin would be doubled from £64 to £128. If this won, you’d make £128 profit on this spin, covering your previous losses of £127 and giving an additional £1 profit on top.
Whilst it might seem exciting to have a £2048 win on your 12th spin, it’s important to realise that your actual overall profit for this ‘Martingale round’ (a run of results between one win and the next) is only £1. That’s despite having been £2047 down from the previous rounds and risking a further £2048 loss on that 12th spin.
The staking pattern for the Martingale Strategy, where you double up every time you lose, is an example of a geometric progression. With this sort of progression, to get the next term in the sequence, you multiply the previous term by a certain number (in this case, this number is 2, as we’re doubling our stake). As you can see from the ‘Stake’ column in the table above, with this sort of progression, the numbers get very big, very quickly.
The History of the Martingale Strategy
The Martingale Strategy is thought to have originated in France in the 18th Century, where it was a popular system with gamblers. How it got its name is uncertain, but it’s been suggested that the word martingale comes from the Provençal expression ‘jouga a la martegalo’, which means “to play in an absurd and incomprehensible way”. You’ll soon see that this is a pretty good description of the strategy.
It’s often suggested that the Martingale Strategy was either named after or popularised by an 18th century London casino owner, John H. Martindale. According to legend, he used to walk around the casino, encouraging his customers to double their bets if they lost. It’s a nice story, but may well not be true.
In the summer of 1891, English gambler and fraudster Charles De Ville Wells visited the Monte Carlo Casino, where it’s said he ‘broke the bank’ by winning more than the 100,000 francs cash reserve of the table, which led to the casino having to suspend play on the table whilst they brought more funds from the casino’s vaults. He claimed to be using an ‘infallible system’, which some people believe to have been the Martingale Strategy.
Why You Shouldn’t Use the Martingale Strategy
There are several reasons why the Martingale Strategy doesn’t work, but first, let’s look at one situation where it does work.
The Martingale Strategy is a perfect system if you have infinite money and play at casinos with no table limit.
With infinite money and no table limits, you’d always be able to keep doubling up until you won, since it’s almost 100% certain that you’ll eventually have a winning spin.
Dragging ourselves back to the real world, where casinos definitely have table limits and, sadly, none of us have infinite wealth, you’ll see there are several very good reasons why the Martingale Strategy doesn’t work.
Gambler’s Fallacy
Gambler’s Fallacy is a commonly-held, but mistaken belief that if an independent and random event has happened less frequently than expected, it’s more likely to happen in the future (or vice versa).
To understand what this actually means, imagine you’re flipping a coin and have seen a run of 5 heads in a row. Instinctively, you might think that 6 heads in a row is very unlikely, so the next flip has a greater chance of landing on tails.
This isn’t the case, since neither the coin nor the Universe have any ‘memory’ of any of the previous results. As long as it’s a fair coin, it will always have the same 50% chance of landing on heads, no matter what’s happened with previous results.
If you have any doubts about this, try coming up with an explanation of how a coin flip could possibly be linked to the previous coin flip, or how the last spin on a roulette table could affect the next spin.
You’ll often see discussions about gambling on roulette where people suggest waiting for a run of one colour at the roulette table before starting the Martingale Strategy on the other colour.
Of course, since each spin is completely independent of all others, it makes no difference at all when you start the strategy - you’ll always have exactly an 18/37 chance of your colour coming up.
If you wait for 5 reds in a row, before starting to bet on black, not only does it make no difference at all to your chances of winning, you’ll also spend much more time waiting for these long runs of reds than you will actually placing any wagers!
In general, the following is true:
For a random and independent event, previous results have no effect on future outcomes.
Examples of random and independent events are coin tosses, roulette spins and spins on online slot machines.
Going a little deeper into this, the misunderstanding arises because people know that there is only a relatively small chance of having a run of the same outcome (for example, flipping a coin 6 times and getting 6 heads). As you’ll see below, this is true:
Probability of getting 6 heads from 6 coin flips = ½ x ½ x ½ x ½ x ½ x ½ = 1/64
This doesn’t tell the full story though. This 1 in 64 chance only applies before flipping the coin the first time. If you’ve already flipped 5 heads, these previous results are irrelevant to any future results. After already flipping 5 heads, the chance of getting the 6th head in a row is 1 in 2, not 1 in 64.
Another name for Gambler’s Fallacy is the Monte Carlo Fallacy, so called because of a particular game of roulette played at the Monte Carlo Casino in 1913, where the ball landed on black an unusually large number of times in a row. The casino’s customers became increasingly convinced that after such a long run of blacks, it was almost certain to land on red soon, so started betting increasing amounts of money on red. Unfortunately for them, the run only ended after black had turned up an astonishing 26 times in a row! Needless to say, lots of people lost a lot of money that night, whilst the casino made a tidy profit.

If you’d been using the Martingale Strategy with a 10p starting stake on that run, betting on red each time, and with a bankroll to cover all the required wagers, you’d be over £6.7 million down after those 26 losses!
But just how likely is it that you’ll have a losing streak that wipes out your entire bankroll when using the Martingale Strategy? Probably more likely than you think!
How Likely Are Long Losing Streaks?
We’ve already seen that there’s only a 1 in 64 chance of flipping a coin six times in a row and getting six heads. Moving onto red or black roulette bets, the chance of winning any particular spin is slightly less than 50%, thanks to the green zero (or, if you’re playing American roulette, the zero and double zero).
With European roulette, which has only one zero, there are 18 reds, 18 blacks and 1 green, so 37 possible outcomes. Betting on black, 18 out of the 37 possible outcomes are winning spins.
Probability of winning = 18/37 = 48.64%
As you’ve already seen, if you have a winning spin, your overall profit each time you is just your original stake, so nothing dramatic happens with winning streaks. With losing streaks, your loss doubles each time you lose, so it’s much more important to look at the chance of a losing streak.
There are 19 outcomes that are not black, so betting on black, the probability of losing is:
Probability of losing 1 spin = 19/37 = 51.4%
Probability of losing 6 spins in a row = 19/37 x 19/37 x 19/37 x 19/37 x 19/37 x 19/37 = 1.83%
This is about a 1 in 54 chance, so it’s not particularly likely that you’ll have 6 losing spins out of 6 wagers. However, if you’re playing roulette, you probably won’t just do 6 spins and walk away. A more important question to ask is how likely is a losing streak of 6 when you’re doing a longer run of spins.
This is a bit more complicated to work out, but here’s a table showing the chance of having at least one losing streak of 6 or more at some point when doing different numbers of spins. The loss you’d have incurred from this losing streak, if you started with a £1 stake, is also included.
Likelihood of a Losing Streak of 6
With a £1 starting stake, your loss from a losing streak of 6 would be £63.
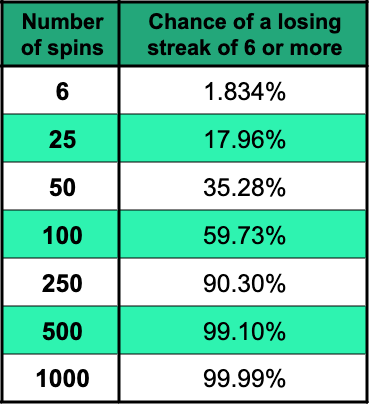
As you can see, if you do 100 spins, there’s a greater than 50% chance that you’ll have a streak of at least 6 losing spins. If you do 1000 spins, it’s almost a dead cert.
But what about longer losing streaks?
Likelihood of a Losing Streak of 7 or 8
With a £1 starting stake, your loss from a losing streak of 7 would be £127.
With a £1 starting stake, your loss from a losing streak of 8 would be £255.
The chance of longer losing streaks is obviously lower for a given number of total spins, but you only need to do a surprisingly small number of spins to be almost certain to hit at least one run of that length or more.
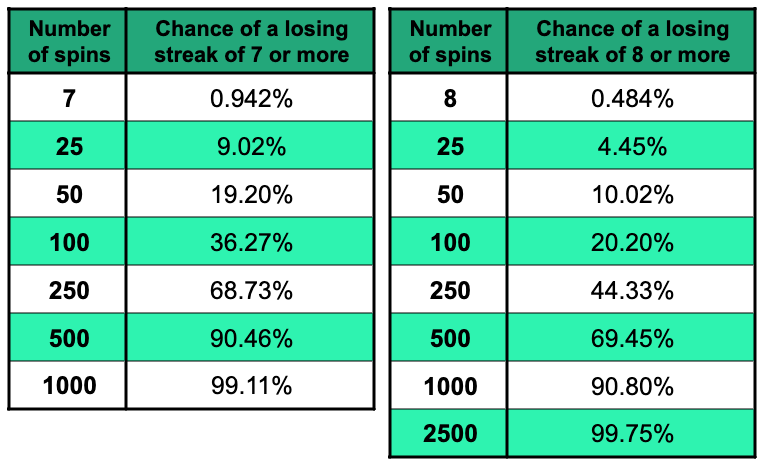
As you can see, if you do 1000 spins, your chance of hitting 7 losing spins in a row is over 99%. If you do 2500 spins, you’ll almost certainly lose 8 or more wagers in a row at least once.
Likelihood of a Losing Streak of 9 or 10
With a £1 starting stake, your loss from a losing streak of 9 would be £511.
With a £1 starting stake, your loss from a losing streak of 10 would be £1023.
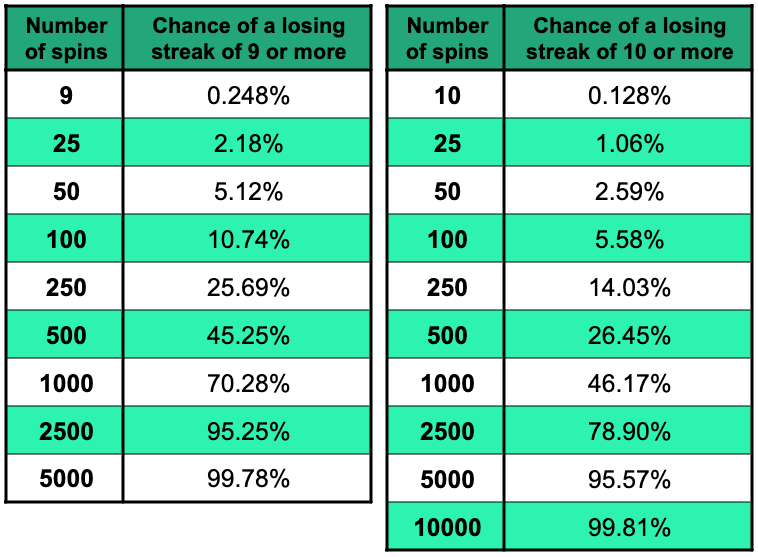
5000 spins makes a losing streak of 9 or more almost certain, and 10000 spins means you’re almost certain to see a losing streak of at least 10.
It’s worth emphasising what’s at stake (no pun intended) if you try the Martingale Strategy. Starting with a £10 stake and doing 10,000 spins, there is a lower than 1 in 500 chance that you won’t end up losing £10,230 or more after hitting a losing streak of 10 in a row!
If you use the Martingale Strategy, the question is when, not if, you’ll hit a catastrophic losing streak.
Now, let’s look at the expected value of the Martingale Strategy. Despite the obvious risks, does it actually give us some kind of edge, or at least improve upon other staking strategies like always staking the same amount?
The Expected Value of the Martingale Strategy
To work out whether a strategy is viable in the long-run, its expected value (EV) can be calculated.
In a casino, the expected value is the average profit or loss you’ll make from a wager.
The expected value takes into account how likely the wager is to win, the profit if it wins, and the loss if it loses.
Coin Flip Expected Value

For a coin flip, the chance of either heads or tails is 50% (0.5). If you’re flipping a fair coin and make £1 profit if it lands on heads and lose £1 for tails, the EV of one flip is:
EV = 0.5 x £1 + 0.5 x -£1 = £0
With the Martingale Strategy, you’d double the stake to £2 if this £1 wager lost. It’s no surprise that the EV for this £2 spin is also £0:
EV = 0.5 x £2 + 0.5 x -£2 = £0
You have no edge with a £1 spin, so also have no edge with a £2 spin. It doesn’t matter what your stake is; the EV will always be £0.
The total EV of your two coin flips, using the Martingale Strategy, is:
Total EV = £0 + £0 = £0
For this coin flip example, the EV will be £0, no matter what staking pattern you use, since the EV of any individual flip is always £0.
Red / Black Roulette Spin Expected Value

The probability of a wager on black winning at roulette is less than 50%, due to the green zero, with 18 winning outcomes out of a possible 37.
Probability of black = 18 / 37 = 0.486 = 48.6%
The expected value of our first £1 spin on black is around -3p:
EV = (18/37) x £1 + (19/37) x -£1 = -£0.027
Assuming that spin loses, we’d now double up to a £2 stake. Here’s the EV for this spin:
EV = (18/37) x £2 + (19/37) x -£2 = -£0.054
As you’d expect, the negative EV is twice as large as it was for the £1 stake. If this spin also loses, we’d again double to £4. The EV for this spin is:
EV = (18/37) x £4 + (19/37) x -£4 = -£0.108
Again, doubling the stake doubles the average loss.
In general, when using the Martingale Strategy:
The expected value for any wager is negative and gets twice as bad each time you double.
In total, you’ve wagered £1 + £2 + £4 = £7. The overall EV of wagering that £7 is just the sum of all of the individual EVs:
Overall EV = -£0.027 - £0.054 - £0.108 = -£0.189
So if wagering £7 with the Martingale Strategy has an EV of -£0.189, what about the EV of just wagering the £7 with a single £7 spin? It’s exactly the same:
EV = (18/37) x £7 + (19/37) x -£7 = -£0.189
Returning to the example of a £10 starting stake Martingale Strategy, after 10 losing spins in a row, we’d need to wager £10,240 for the 11th spin to continue. The Expected Value of this spin is:
EV = (18/37) x £10240 + (19/37) x -£10240 = -£276.76
Another way to check the expected value of wagering £10240 on roulette is to use an EV Calculator. Roulette has a Return To Player (RTP) of 97.3% to 1 decimal place, but it’s actually a recurring decimal, so a more precise RTP is entered below, to give the correct expected value:
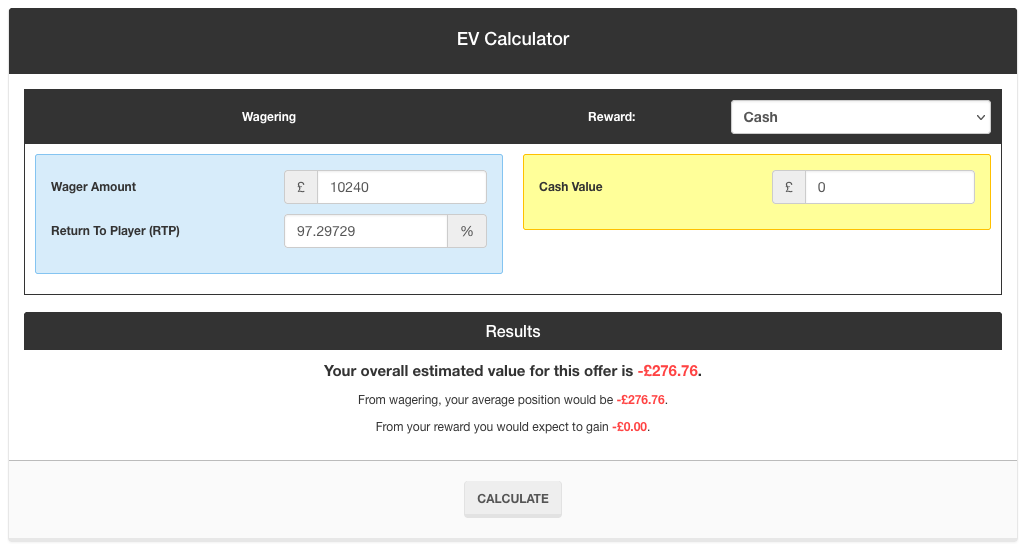
On average, you’ll lose £276.76 from a £10240 roulette spin on black. This clearly isn’t worth doing in the long-run, and it’s slightly worse than the total negative EV of all 9 previous spins added together, which comes to -£276.49.
The total EV of all 11 spins would be the sum of the EVs for each individual spin, which comes to £553.24.
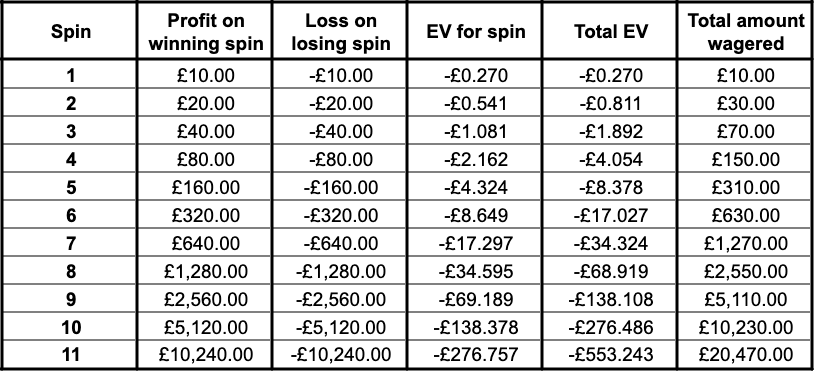
The total amount wagered across those 11 spins is £20,470. Let’s see how using the Martingale Strategy to wager this amount compares to just doing one £20,470 spin (or 20,470 £1 spins):
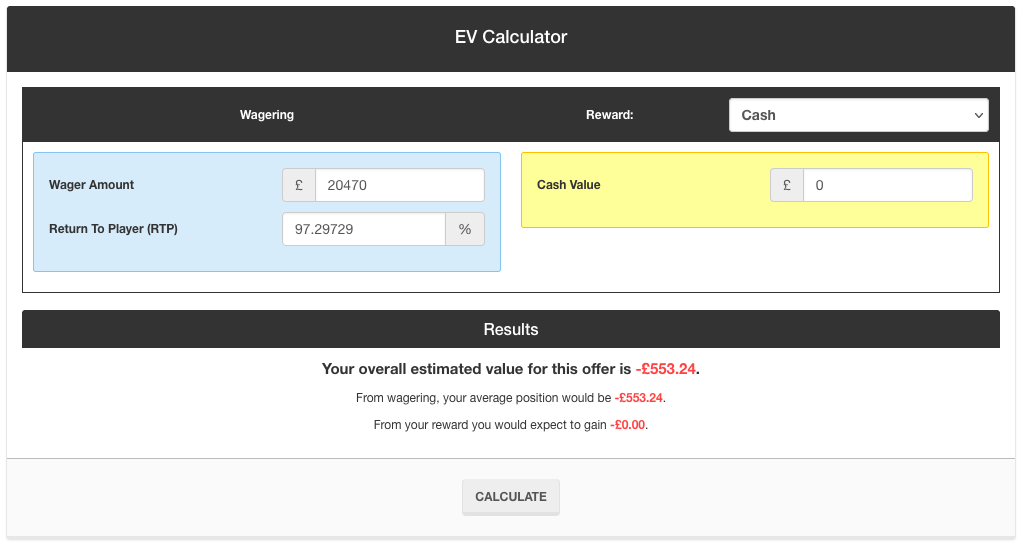
As you can see, the EV is still the same. For any amount of cash wagered, the EV is identical whether you’re using the Martingale Strategy or any other system of wagering.
Some reasons why people might still continue with the Martingale Strategy even after a long run of losses are:
- They aren’t aware that the strategy has negative expected value.
- They believe the chances of hitting a losing streak long enough to wipe out their bankroll is so small as to be insignificant (we’ve seen that this definitely isn’t the case).
- As they’re down a lot of money, they believe that the best strategy to recover that loss is to do another spin to try to cover this and still come out with a profit if this wins. Otherwise, they’ll feel that they have ‘wasted’ the amount of money already lost.
The last point is an example of the Sunk Cost Fallacy, which we’ll look at next.
Sunk Cost Fallacy
A sunk cost is a cost that has already been incurred and can’t be recovered.

An example of a sunk cost is if you’ve just had a series of expensive repair bills on your car and it develops a serious fault which will be very expensive to fix, and more than the car is worth.
The reality is you’d be better off ‘cutting your losses’, selling the car for scrap or parts and using the money you’d have used for the repairs to buy another car.
Thinking logically, since you can’t do anything about these previous costs, they shouldn’t affect your future decisions.
However, because you’ve spent lots of money, time, and effort getting the car fixed, there’s naturally a strong temptation to cough up for the latest repair as well.
Otherwise, you might think you’ve wasted your money on those other bills.
On the other hand, if you’d had no significant expenses on the car and were then faced with that massive bill, you’d probably decide that it’s not worth repairing.
The sunk cost fallacy is our tendency to continue with an endeavour that we’ve invested money, time, effort or emotional energy into, even if the costs of continuing outweigh the benefits.
Returning to the roulette example, if you’re already running at a £10,230 loss, the logical thing to do is to stop wagering and accept this loss.
Obviously, an even more logical decision would be to never have started the Martingale Strategy in the first place!
We know that this £10,240 spin has a very large negative EV and isn’t worth doing. However, as the losses mount up, so does the temptation to wager ever increasing amounts to cover these losses.
Rather than cutting their losses and walking away with that £10,230 loss, many people will (assuming they have the bankroll to cover it), continue with the Martingale Strategy and place the next wager for £10,240, hoping that this one wins.
Something else to factor in with the Martingale Strategy is that casinos all have table limits, which put a ceiling on the maximum wager you can place.
Here are a couple of different live casino roulette tables. Both have a minimum stake of 10p, with one having a maximum stake of £1,800 and the other £10,000.
Exclusive Roulette
Range of possible stakes: £0.10 - £1,800.

Spread Bet Roulette
Range of possible stakes: £0.10 - £10,000.

If you'd started with 10p spins on the Martingale Strategy on the Spread Bet Roulette table, and had a losing streak of 17, you’d be £13,017.10 down, with a stake over £13,000 needed for your 18th spin. Due to the £10,000 table limit, you wouldn’t be able to place this wager.
Obviously, you could try to find a table with a higher limit, or see if you can place a sports bet at odds of 2.0 with this stake. The problem is that all casinos have table limits, and bookmakers also apply stake restrictions to their customers, so you might find nowhere to place your bet.
It’s a widely held belief that table limits were introduced by casinos to protect them from customers using the Martingale Strategy.
The reality is that casinos aren’t at risk from Martingale gamblers. Someone playing the Martingale with a £1,000 starting stake who was on a losing streak of 10 in a row would have a stake of £1,024,000 for their 11th wager. The casino would easily be able to cover this, since they would have just made £1,023,000 from that gambler’s previous 10 losing spins.
Even if it wins, they will only end up with an overall loss for that customer for that Martingale sequence of £1,000. If the customer loses once again, the casino makes a nice additional profit of over £1 million on that one spin.
It could be argued that table limits benefit casinos when players have a long losing streak using the Martingale Strategy by not allowing them to continue to double their stakes.
If the player is £13,000 down with a £13,000+ wager required for the next spin, a £10,000 table limit prevents the player from making that spin, and the casino makes a £13k profit.
However, the main reason casinos have table limits is because they are at risk from lucky players who win large amounts relative to the amount of money that can be covered by that particular casino. For example, someone staking the maximum £10,000 on a single number on the Spread Bet Roulette table would win 36x their stake if their number comes up, with a £360,000 payout.
When the Martingale Strategy is discussed, you’ll often see casino table limits mentioned as the main problem with the system. However, it’s really the inevitability of a bankroll-busting losing streak that is the Martingale’s biggest downfall.
Simulation Results
A great way to test out a strategy is by running a simulation on a computer, and it’s ideal for the Martingale Strategy. With this in mind, I created a casino simulator to put the strategy to the test.
The nature of the Martingale means that you’ll tend to have lots of small wins and a few big losses. Running the simulation for long enough, no matter what bankroll and initial stake you use, you’ll always have a catastrophic losing streak that wipes out your bankroll.
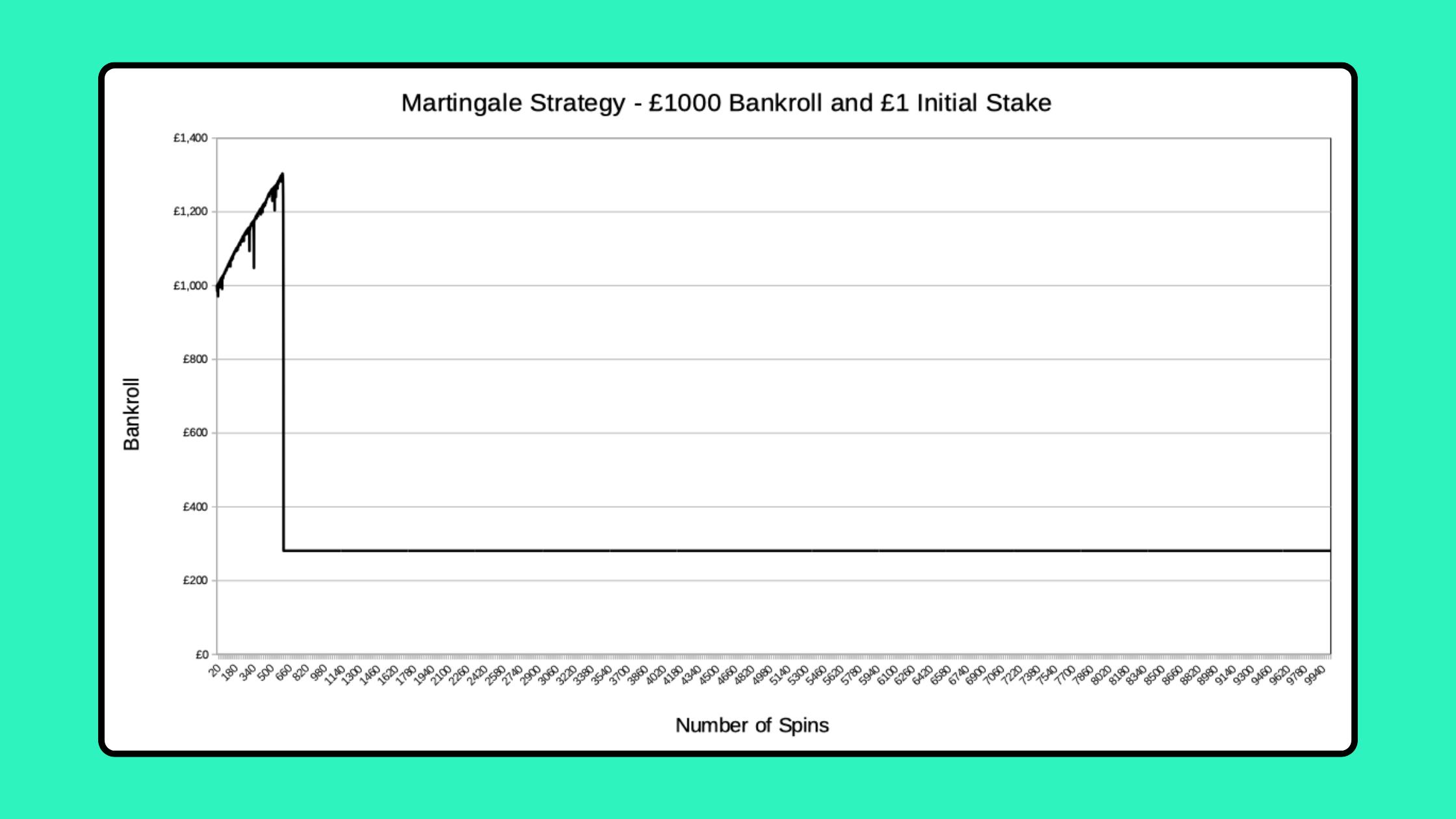
Simulation of 100 Spins
Here, you can see a typical pattern for what can happen when wagering £100 using the Martingale Strategy, starting with a bankroll of £1000 and with a £1 starting stake:
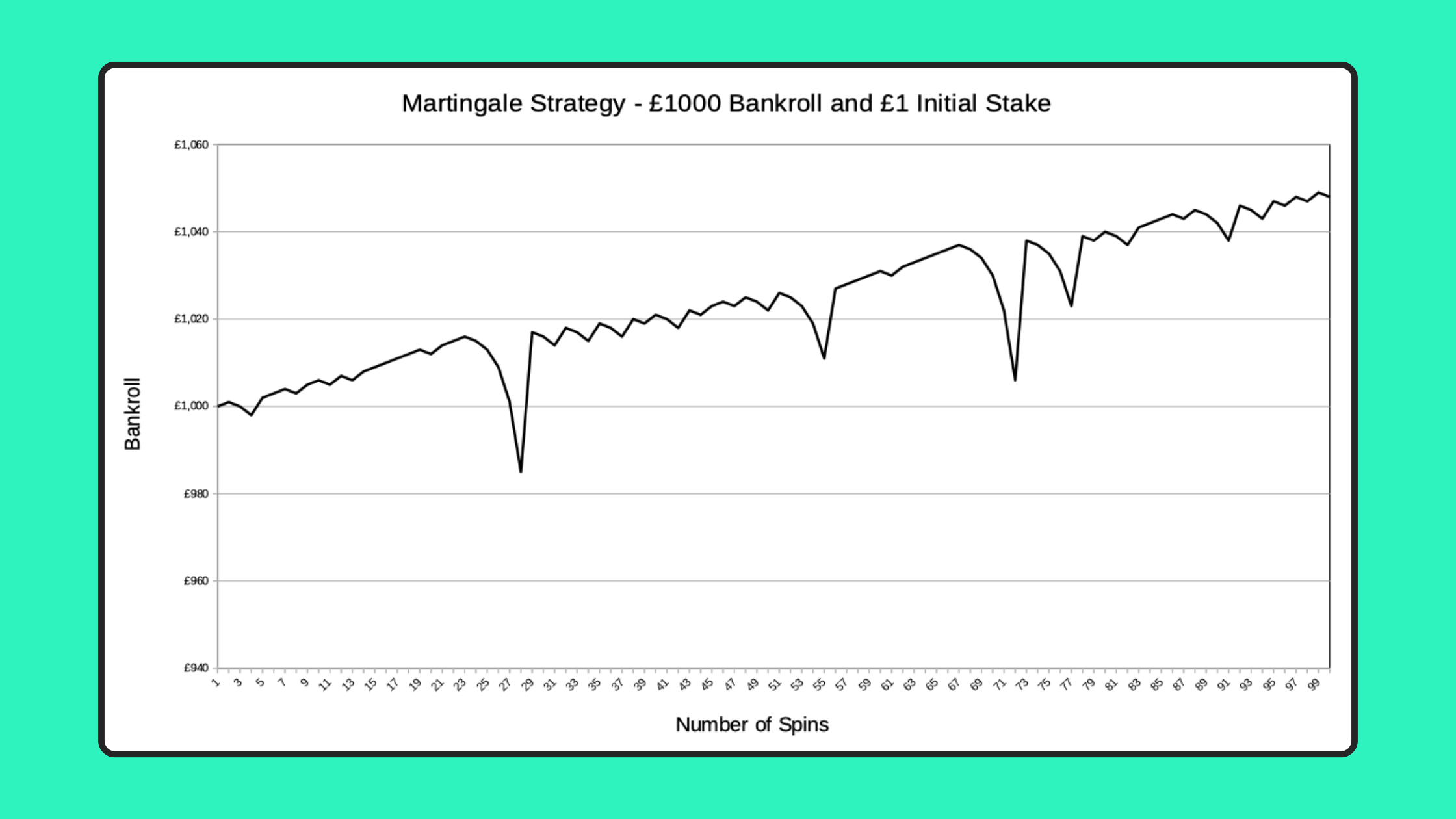
This very small sample size could make the Martingale appear to be a potentially valid strategy, especially if you just look at one simulation.
We’ve seen that the chance of a losing streak of 10 or more, which would lead to a £1023 loss that uses up your £1000 bankroll is 5.58% (about 1 in 18).
Therefore, we’d expect to make a profit 17 times out of 18 here, so more often than not, you’ll have a result like the one above, when wagering £100. The problem is that on the other 1 occasion, you lose your entire £1000 bankroll!
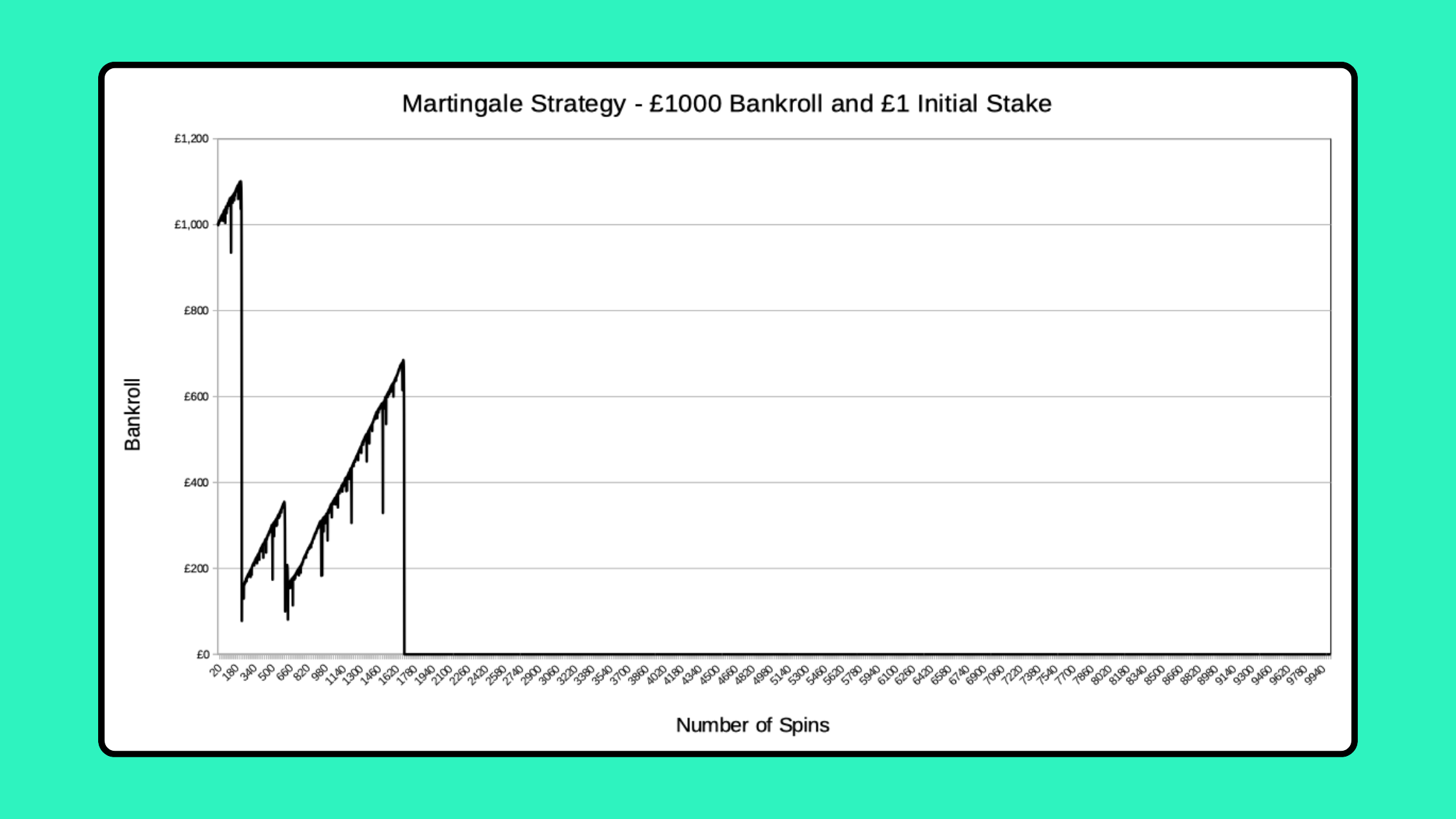
Simulations of 1,000 Spins
The more spins you do, the greater chance you have of hitting a losing streak of 10 or more. With 1000 spins, there’s a 46.17% chance of having 10 losses in a row, so you’d expect to lose your entire bankroll about half the time.
I’ve set the simulator to run a slightly modified Martingale so that, if you don’t have enough remaining bankroll to cover the full doubled stake required, you go ‘all in’ and bet all your remaining money. This can lead to a few last ditch ‘rescues’, and it makes it a little more likely you’ll get through 100 spins, compared to stopping if you can’t double up.
Here are a couple of typical simulation results:
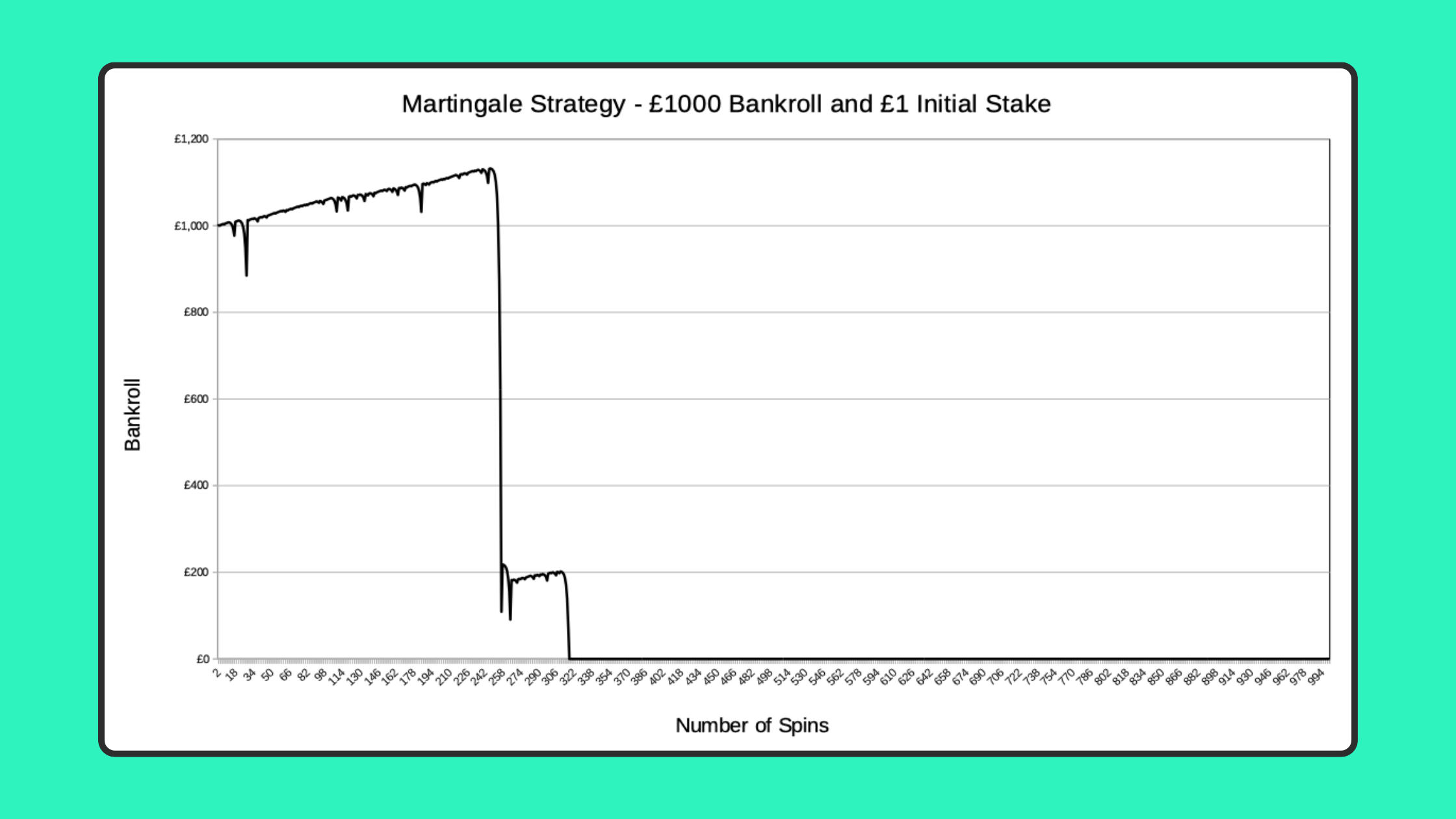
This one is an example of ‘it was going so well’. If you use the Martingale for long enough, you’ll inevitably have a losing streak like this, where you lose your entire bankroll.
Ultimately, all simulations, and all sufficiently long real Martingale runs, eventually end like this one!
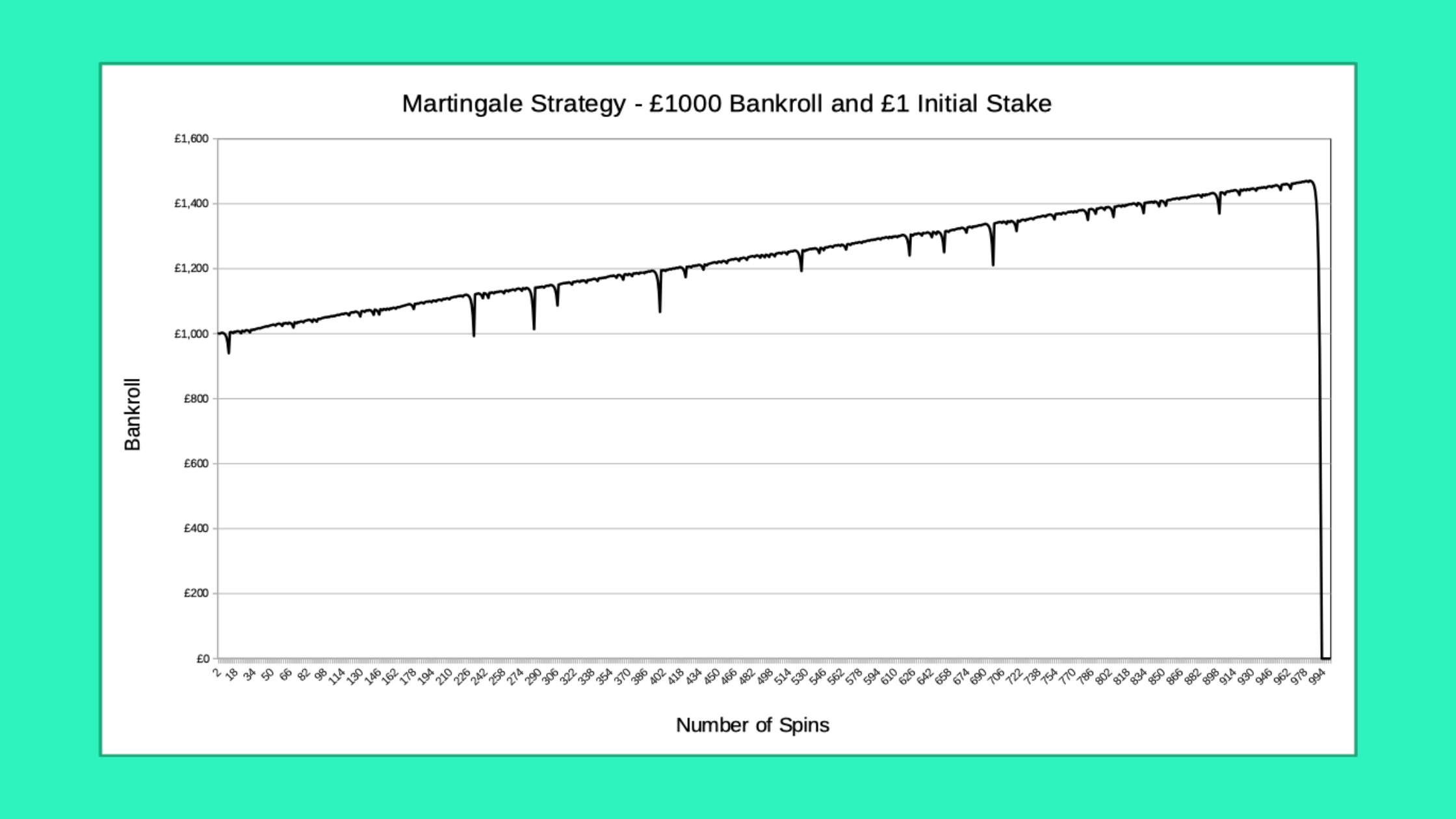
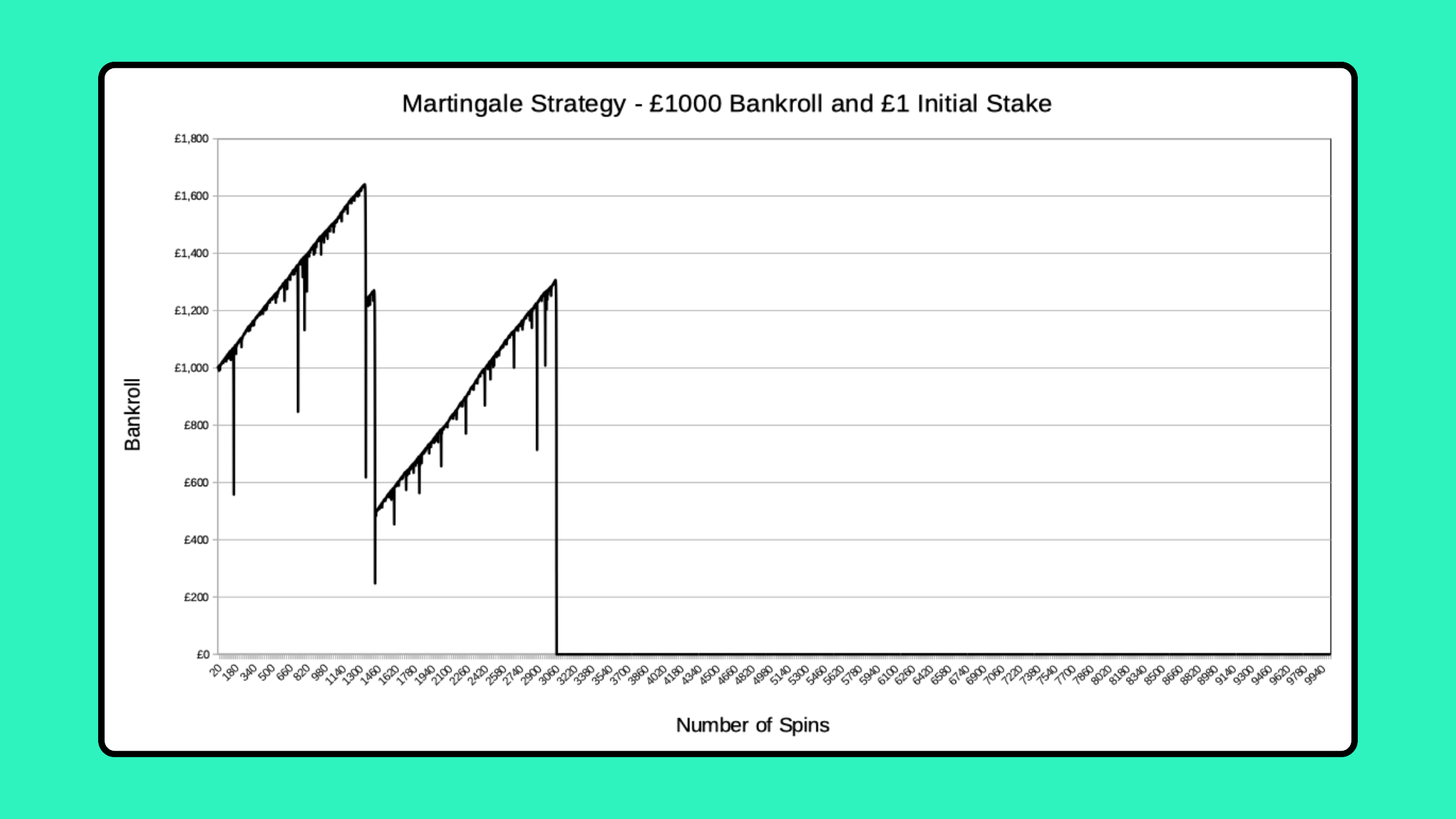
Simulations of 10,000 Spins
Moving onto simulations of 10,000 spins, there’s now only a 99.81% chance of avoiding a losing streak of 10 or more, with a loss of over £1000.
The modified strategy of staking your entire bankroll if you can’t double up tends to extend these runs, but you’re only delaying the inevitable.
Here’s a fairly rare example of a run of 10,000 spins that ends with a profit:
These two are much more typical, and almost all simulations of 10,000 spins with a £1 initial stake and £1000 bankroll will end with you losing everything.
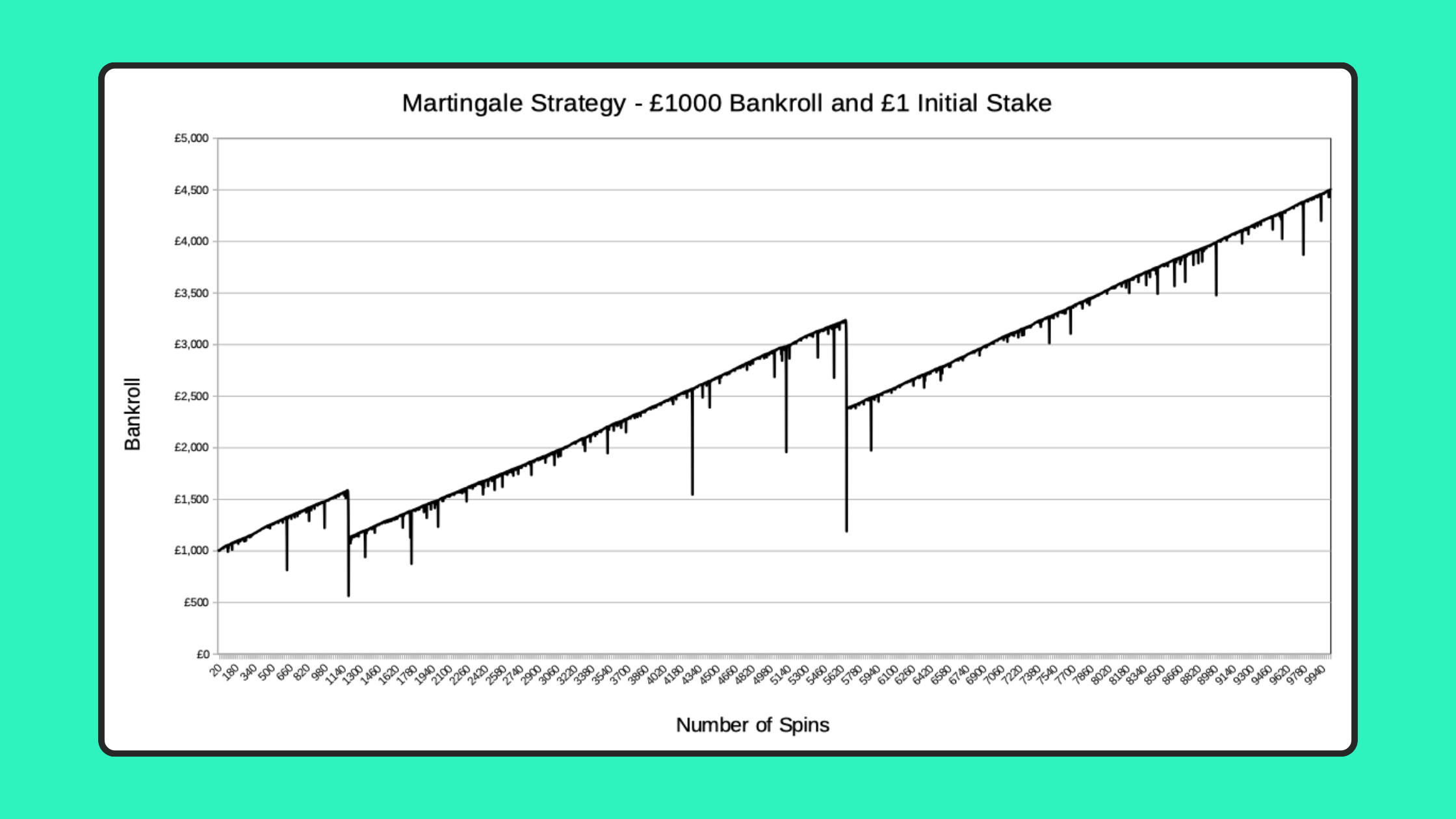
Individual simulations tell us a lot about what these Martingale runs can look like, but it’s also interesting to plot multiple simulations on the same graph. Here you can see the result of 100 simulations of 10,000 spins, again starting with £1 spins and a £1,000 bankroll.
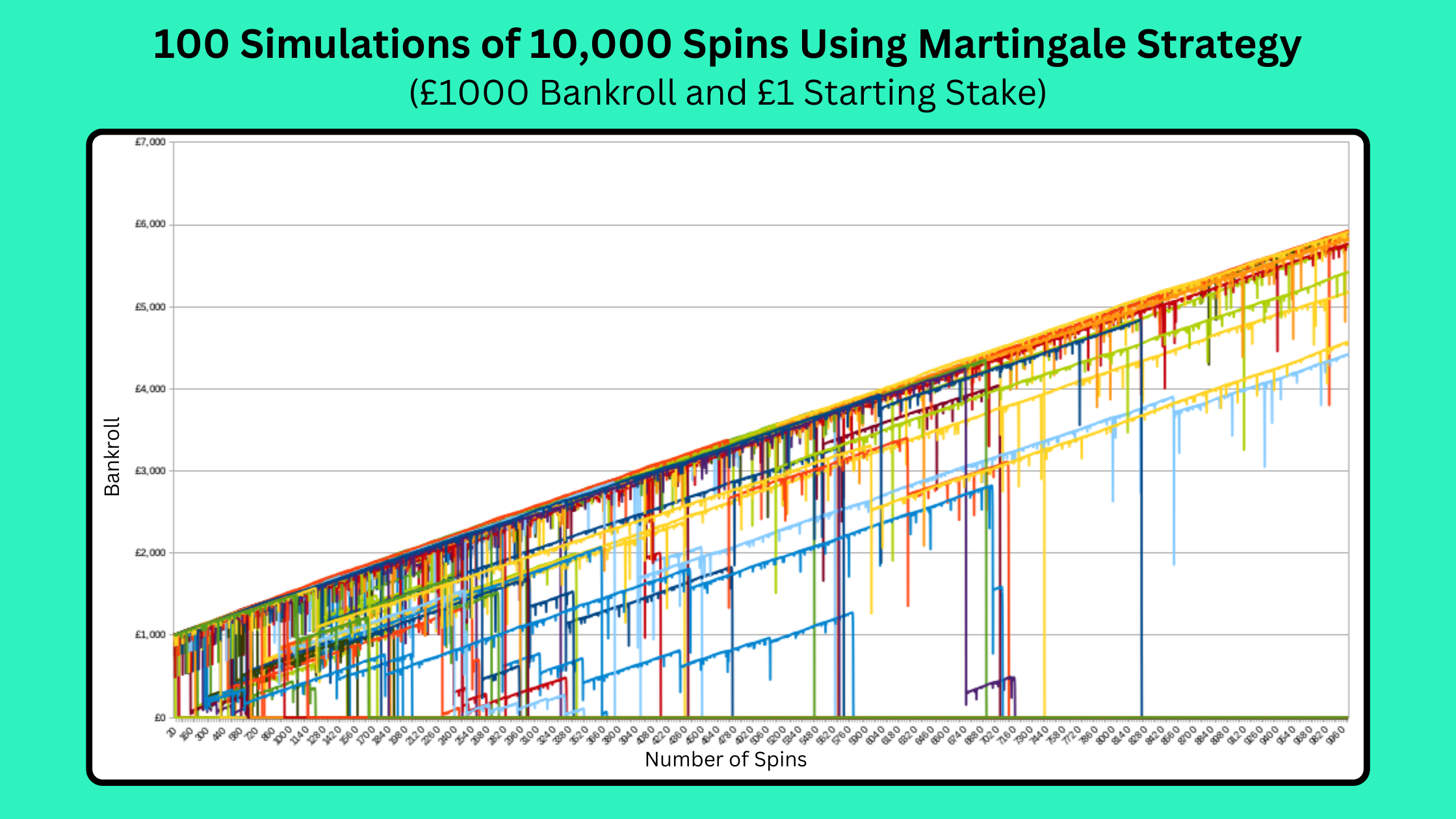
Whilst the graph probably wouldn’t look out of place at a modern art exhibition, it gives a good insight into what tends to happen over the long-term when using the Martingale Strategy.
If you’d wagered your own money on 100 Martingale runs like this, you’d have started with a total of £100,000. The good news is that 13 of the 100 runs ended with a profit, with a total profit on these runs of £59,208. The bad news is that you’d have lost your entire £1000 bankroll the other 87 times, for a loss of £87,000. Overall, you’d be £27,792 down from your £100k starting pot!
Alternative Martingale Strategies
We’ve seen that the basic Martingale Strategy doesn’t work, but are there any improved versions that are any better?
One idea that might be appealing is using the Martingale to try to double your bankroll. There’s a great video that covers this idea:
Gambling with the Martingale Strategy - Numberphile
I’ve set my simulator to replicate this strategy. Again, the simulation starts with a £1,000 bankroll and £1 initial stake size. In line with the strategy used in the video, the Martingale Strategy is used until you either double your starting bankroll or have a £1,000+ losing spin.
Some runs will end with a successful doubling of your stake, like here:
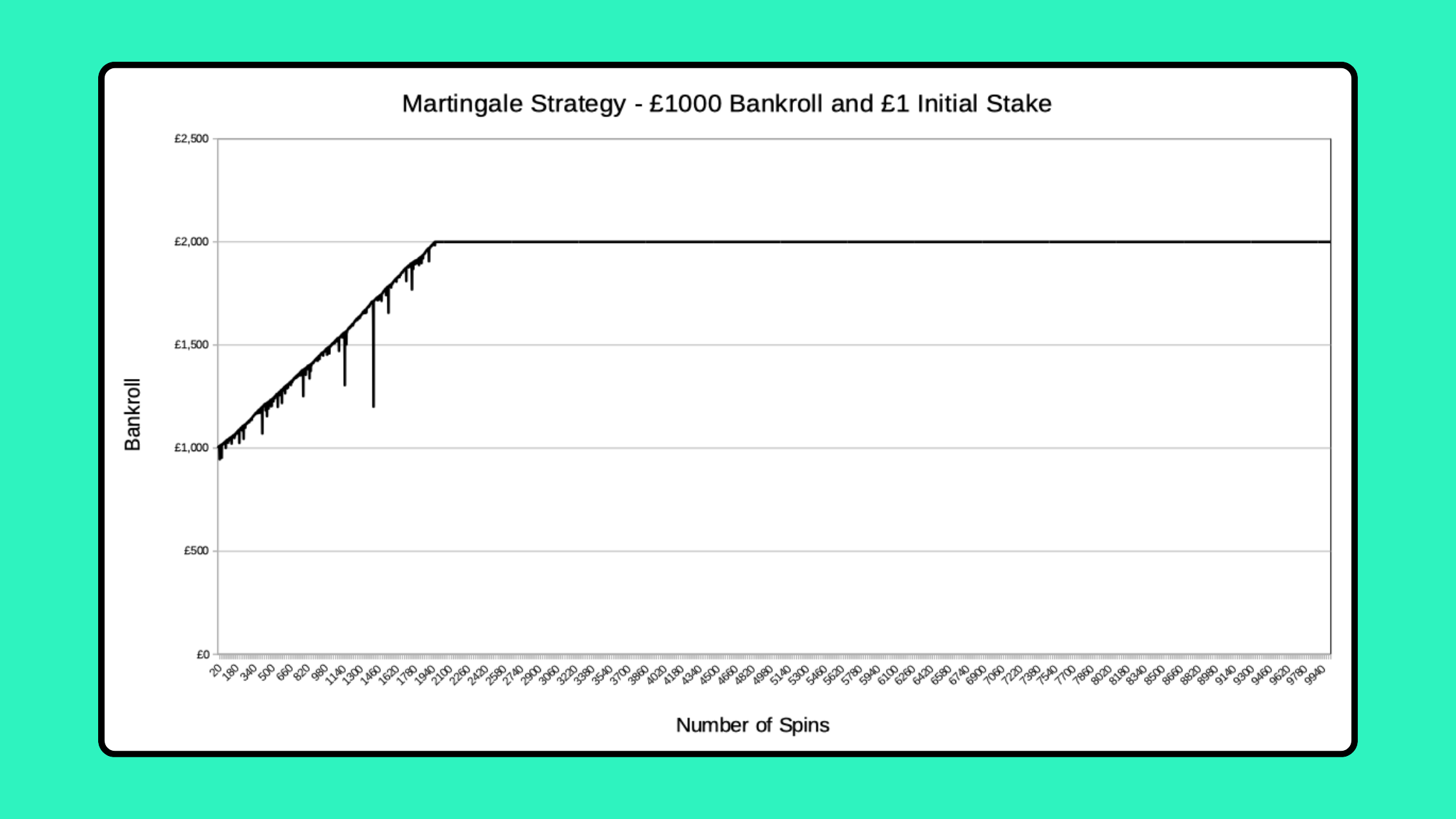
Others end with a losing spin of £1,024 or more:
An interesting question, covered in the video, is how likely are you to double your bankroll using this strategy? To keep the maths more simple, we’re assuming there’s a 50% chance of winning. This could be a coin toss or a roulette table with no green zero (you won’t find tables like this in real casinos for obvious reasons!)
Starting with a bankroll of £100 and £1 initial stake, there’s a 36.6% chance of doubling your bankroll to £2,000.
If start with more money, your chance of doubling this bankroll increases, but only very slightly. Starting with £1,000, the chance of doubling your bankroll only increases to 36.8%. In fact, no matter how much bankroll you start with, the likelihood of doubling your money never goes above 36.8%.
Rather than using the Martingale Strategy, you’d be much better off just gambling your entire £1,000 bankroll on one coin flip or roulette spin, since you’d then have a 50% chance of doubling your bankroll! And no, we don't advise you do this either!
With roulette, your chance of doubling your stake would be even worse than 36.8% due to the green zero.
You’ll see many other suggestions of ‘improved’ Martingale variants that supposedly work better than the ‘classic’ version. Ultimately though, they all fall down for the reasons we’ve seen. They’ll always be negative expected value systems, since you can’t beat the house edge with any staking strategy.
Conclusion
Many people have tried the Martingale Strategy over the years, and still do to this day.
You’ll often see it discussed online, with people relaying stories of variable levels of success - some apparently making a reasonable profit and others losing their entire bankroll.
Of course, whilst interesting to read and giving a little insight into how the Martingale Strategy can play out in different situations, online anecdotes certainly aren’t the best way to decide how effective a system is.
This is why it’s so important to have a good understanding of whether or not the Martingale is actually an effective system, and what the risks are.
To summarise, we know that the Martingale Strategy doesn’t work. Here are some of the key points:
- The Martingale Strategy would only be an effective strategy if you had infinite money and casinos had no table limits.
- The chance of having a losing streak that leads to you losing your entire bankroll is much higher than most people think, increases rapidly as the length of run increases, and approaches 100% for longer runs.
- Martingale Strategies all have negative expected value, which is the same as the expected value of wagering an equivalent amount using any other staking pattern.
- The Martingale Strategy is a high risk and low reward strategy, with small gains being common in the short term but very large losses being inevitable in the long term.
- If you use the Martingale, your average stake size is likely to be much higher than if you always staked a fixed amount, and you’re likely to lose far more money.
- When playing roulette, each spin is completely independent of all other spins. Having a long run of reds does not affect the chance of the next spin being black.
The good news is that you can actually give yourself the edge over casinos and bookmakers, and make long-term profits.
With Outplayed membership, you can find out everything you need to know about a range of methods to make long-term profits from bookmakers and casinos, from Matched Betting to casino offers and value betting.
Updated: 8 Sep 2025
The Author
Simon has helped thousands of members profit from Matched Betting using both his passion for writing and desire to understand how things work. He has used his mathematical and analytical skills to create several guides, calculators, betting and casino tools to make the process of Matched Betting easier for newcomers and experienced members alike.

